Fibonacci numbers and the Golden Ratio are NOT the same thing…but you knew that :)

Closed-form expression

Like every sequence defined by linear recurrence,^[16] the Fibonacci numbers have a closed-form solution. It has become very well known as Binet‘s formula, even though it was already known by Abraham de Moivre:^[17]

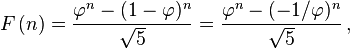
$Fleft(nright) = {{varphi^n-(1-varphi)^n} over {sqrt 5}}={{varphi^n-(-1/varphi)^{n}} over {sqrt 5}}, ,$

where

$varphi = frac{1 + sqrt{5}}{2} approx 1.61803,39887dots,$

is the golden ratio (sequence A001622 in OEIS).

That

$1-varphi=-1/varphi,$

follows from the defining equation above.

The Fibonacci recursion

$F(n+2)-F(n+1)-F(n)=0,$

is similar to the defining equation of the golden ratio in the form

$x^2-x-1=0,,$

which is also known as the generating polynomial of the recursion.

via en.wikipedia.org